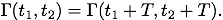Cyclostationary Optical Fields

Overview:

Optical coherence theory, or statistical optics, is the theory of the random fluctuations present in most optical fields. Statistical optics is usually formulated under the assumptions of stationarity (at least in the wide sense) and ergodicity. These two assumptions allow one to make meaningful statements about the field statistics from direct (time-averaged) measurements of the field intensity. The assumption of stationarity implies that the field statistics do not vary with time - a fair assumption for the light emitted by cw lasers, distant stars, and blackbody radiators. Ergodicity allows one to relate time-averaged measurements to statistically meaningful quantities.

For stationary fields, the Weiner-Khintchine-Einstein (WKE) theorem is used to relate measurements of the spectral density of the field to the field's autocorrelation properties. The WKE theorem states that, for stationary fields, the field is uncorrelated at distinct frequencies (light at each frequency is independent of the light at all other frequencies) and that the Fourier transform of the spectrum at a point in space is the autocorrelation of field at that point.

The major drawback of the traditional statistical optics approach, however, is that only a small subset of realizable fields can be assumed stationary. Pulsed fields obviously fail the most obvious requirement of stationarity - the pulse envelope is time-varying. There are a number of ways to relax the time-invariance implicit in the assumption of stationarity - our research centers on the assumption of cyclostationary fields to describe a pulse train.

Cyclostationary fields are fields whose field statistics are shift invariant with respect to a specific time shift, T, i.e.

One sees immediately that cyclostationary fields are, in some sense, periodic. A cyclostationary field model is ideal for describing a train of equally-spaced optical pulses. This periodicity implies a modification of the WKE theory: the field is correlated across frequencies separated by the repetition frequency (1/T) or multiples of the repetition frequency and uncorrelated for any other pairs of frequencies.

Our work has looked at detection models for cyclostationary fields in a variety of measurement devices [1], interferometry with cyclostationary plane waves [2] and beams [4], and propagation-induced, correlation-dependent changes in the spectra and cross-spectra of cyclostationary fields [3].

Collaborators:

We are lucky to be able to collaborate with Prof. Randy A. Bartels at Colorado State University. He is an expert in high harmonic generation (HHG) and other experimental methods in optical pulse generation.

References:

1. Observable coherence theory for statistically periodic fields
   B. J. Davis
   Physical Review A,  Vol. 76,  043843  (2007)  PDF
   
2. Optical interferometry with pulsed fields
   R.W. Schoonover, B.J. Davis, R.A. Bartels and P.S. Carney
   Journal of Modern Optics,  Vol. 55,  pp. 1541-1556  (2008)  PDF  
   
3. The generalized Wolf shift for cyclostationary fields
   R.W. Schoonover, B.J. Davis and P.S. Carney
   Optics Express,  Vol. 17,  pp. 4705-4711  (2009)  PDF
   
4. Propagation of spatial coherence in fast pulses
   R.W. Schoonover, B.J. Davis, R.A. Bartels and P.S. Carney
   Journal of the Optical Society of America A,  accepted (2009)